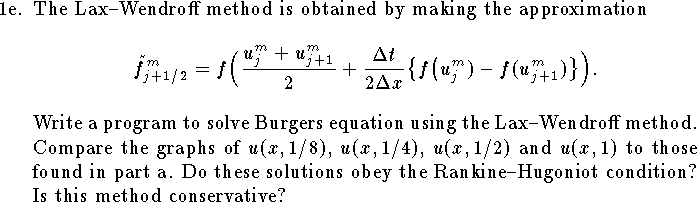Programming Assignment Three
Your work should be presented in the form of a typed report using clear and
properly punctuated English. Where appropriate include full program listings
and output. If you choose to work in a group of two, please turn in
independently prepared reports.
![\def\R{{\bf R}}
\def\Z{{\bf Z}}
\item{1a.} Consider Burgers equation
$$u_t+2u u_x=0\quad \hbox{where $x\in[0,2\pi]$ and $t\ge 0$}$$
with initial condition
$u(x,0)=u_0(x)$ and periodic boundary
conditions $u(0,t)=u(2\pi,t)$.
Non-zero solutions to this equation develop shock discontinuities
in finite time at which point they become non-unique.
A physically relevant solution may
be obtained as the limit of
solutions to the viscous Burgers
equation $$u_t-\nu u_{xx}+2u u_x=0$$
as $\nu\to 0$.
Solve the viscous Burgers equation with
$u_0(x)=2+3\sin x$
for $\nu=0.5$, $0.25$ and $0.125$.
Compare the graphs of $u(x,1)$ for each of these
values of $\nu$. Do these graphs converge?
Can you compute a solution for $\nu=0.01$?
What about for $\nu=0.001$?](a3-1.gif)
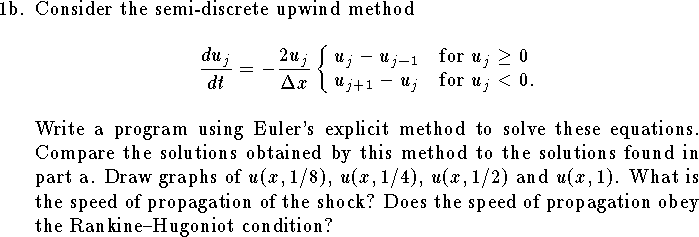

![\item{1d.}
Define the averages
$$
\tilde f^m_{j+1/2}={1\over \Delta t}\int_{t_m}^{t_{m+1}}
f\big(u(x_{j+1/2},t)\big)d t$$
and
$$
\tilde u^m_j={1\over \Delta x}
\int_{x_{j-1/2}}^{x_{j+1/2}} u(x,t_m) dx.
$$
Derive the exact mathematical identity
$$
\tilde u_j^{m+1}=\tilde u_j^{m}-{\Delta t\over \Delta x}
\big(\tilde f^m_{j+1/2}-\tilde f^m_{j-1/2}\big)
$$
by integrating the hyperbolic conservation law
$u_t+\partial_x f(u)=0$
over the intervals $[t_m,t_{m+1}]$ and $[x_{j-1/2},x_{j+1/2}]$
in time and space.](a3-4.gif)

Last Updated:
Sun Apr 27 02:31:28 PDT 2003
![\def\R{{\bf R}}
\def\Z{{\bf Z}}
\item{1a.} Consider Burgers equation
$$u_t+2u u_x=0\quad \hbox{where $x\in[0,2\pi]$ and $t\ge 0$}$$
with initial condition
$u(x,0)=u_0(x)$ and periodic boundary
conditions $u(0,t)=u(2\pi,t)$.
Non-zero solutions to this equation develop shock discontinuities
in finite time at which point they become non-unique.
A physically relevant solution may
be obtained as the limit of
solutions to the viscous Burgers
equation $$u_t-\nu u_{xx}+2u u_x=0$$
as $\nu\to 0$.
Solve the viscous Burgers equation with
$u_0(x)=2+3\sin x$
for $\nu=0.5$, $0.25$ and $0.125$.
Compare the graphs of $u(x,1)$ for each of these
values of $\nu$. Do these graphs converge?
Can you compute a solution for $\nu=0.01$?
What about for $\nu=0.001$?](a3-1.gif)
![\def\R{{\bf R}}
\def\Z{{\bf Z}}
\item{1a.} Consider Burgers equation
$$u_t+2u u_x=0\quad \hbox{where $x\in[0,2\pi]$ and $t\ge 0$}$$
with initial condition
$u(x,0)=u_0(x)$ and periodic boundary
conditions $u(0,t)=u(2\pi,t)$.
Non-zero solutions to this equation develop shock discontinuities
in finite time at which point they become non-unique.
A physically relevant solution may
be obtained as the limit of
solutions to the viscous Burgers
equation $$u_t-\nu u_{xx}+2u u_x=0$$
as $\nu\to 0$.
Solve the viscous Burgers equation with
$u_0(x)=2+3\sin x$
for $\nu=0.5$, $0.25$ and $0.125$.
Compare the graphs of $u(x,1)$ for each of these
values of $\nu$. Do these graphs converge?
Can you compute a solution for $\nu=0.01$?
What about for $\nu=0.001$?](a3-1.gif)
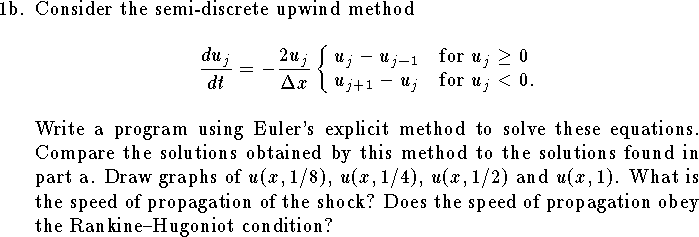

![\item{1d.}
Define the averages
$$
\tilde f^m_{j+1/2}={1\over \Delta t}\int_{t_m}^{t_{m+1}}
f\big(u(x_{j+1/2},t)\big)d t$$
and
$$
\tilde u^m_j={1\over \Delta x}
\int_{x_{j-1/2}}^{x_{j+1/2}} u(x,t_m) dx.
$$
Derive the exact mathematical identity
$$
\tilde u_j^{m+1}=\tilde u_j^{m}-{\Delta t\over \Delta x}
\big(\tilde f^m_{j+1/2}-\tilde f^m_{j-1/2}\big)
$$
by integrating the hyperbolic conservation law
$u_t+\partial_x f(u)=0$
over the intervals $[t_m,t_{m+1}]$ and $[x_{j-1/2},x_{j+1/2}]$
in time and space.](a3-4.gif)